Train a Bayesian Neural Network in Three Minutes

In this tutorial, we will train a variational inference Bayesian Neural Network (BNN) LeNet classifier on the MNIST dataset.

Foreword on Bayesian Neural Networks

Bayesian Neural Networks (BNNs) are a class of neural networks that estimate the uncertainty on their predictions via uncertainty on their weights. This is achieved by considering the weights of the neural network as random variables, and by learning their posterior distribution. This is in contrast to standard neural networks, which only learn a single set of weights, which can be seen as Dirac distributions on the weights.

For more information on Bayesian Neural Networks, we refer the reader to the following resources:

• Weight Uncertainty in Neural Networks ICML2015

• Hands-on Bayesian Neural Networks - a Tutorial for Deep Learning Users IEEE Computational Intelligence Magazine

Training a Bayesian LeNet using TorchUncertainty models and Lightning

In this part, we train a Bayesian LeNet, based on the model and routines already implemented in TU.

1. Loading the utilities

To train a BNN using TorchUncertainty, we have to load the following modules:

• our TUTrainer

• the model: bayesian_lenet, which lies in the torch_uncertainty.model

• the classification training routine from torch_uncertainty.routines

• the Bayesian objective: the ELBOLoss, which lies in the torch_uncertainty.losses file

• the datamodule that handles dataloaders: MNISTDataModule from torch_uncertainty.datamodules

We will also need to define an optimizer using torch.optim and Pytorch’s neural network utils from torch.nn.

from pathlib import Path

from torch import nn, optim

from torch_uncertainty import TUTrainer
from torch_uncertainty.datamodules import MNISTDataModule
from torch_uncertainty.losses import ELBOLoss
from torch_uncertainty.models.lenet import bayesian_lenet
from torch_uncertainty.routines import ClassificationRoutine

2. The Optimization Recipe

We will use the Adam optimizer with the default learning rate of 0.001.

def optim_lenet(model: nn.Module):
    optimizer = optim.Adam(
        model.parameters(),
        lr=1e-3,
    )
    return optimizer

3. Creating the necessary variables

In the following, we instantiate our trainer, define the root of the datasets and the logs. We also create the datamodule that handles the MNIST dataset, dataloaders and transforms. Please note that the datamodules can also handle OOD detection by setting the eval_ood parameter to True. Finally, we create the model using the blueprint from torch_uncertainty.models.

trainer = TUTrainer(accelerator="cpu", enable_progress_bar=False, max_epochs=1)

# datamodule
root = Path("data")
datamodule = MNISTDataModule(root=root, batch_size=128, eval_ood=False)

# model
model = bayesian_lenet(datamodule.num_channels, datamodule.num_classes)

4. The Loss and the Training Routine

Then, we just have to define the loss to be used during training. To do this, we redefine the default parameters from the ELBO loss using the partial function from functools. We use the hyperparameters proposed in the blitz library. As we are train a classification model, we use the CrossEntropyLoss as the likelihood. We then define the training routine using the classification training routine from torch_uncertainty.classification. We provide the model, the ELBO loss and the optimizer to the routine.

loss = ELBOLoss(
    model=model,
    inner_loss=nn.CrossEntropyLoss(),
    kl_weight=1 / 10000,
    num_samples=3,
)

routine = ClassificationRoutine(
    model=model,
    num_classes=datamodule.num_classes,
    loss=loss,
    optim_recipe=optim_lenet(model),
    is_ensemble=True
)

5. Gathering Everything and Training the Model

Now that we have prepared all of this, we just have to gather everything in the main function and to train the model using our wrapper of Lightning Trainer. Specifically, it needs the routine, that includes the model as well as the training/eval logic and the datamodule The dataset will be downloaded automatically in the root/data folder, and the logs will be saved in the root/logs folder.

trainer.fit(model=routine, datamodule=datamodule)
trainer.test(model=routine, datamodule=datamodule)

/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/lightning/pytorch/trainer/connectors/data_connector.py:424: The 'val_dataloader' does not have many workers which may be a bottleneck. Consider increasing the value of the `num_workers` argument` to `num_workers=3` in the `DataLoader` to improve performance.
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/lightning/pytorch/trainer/connectors/data_connector.py:424: The 'train_dataloader' does not have many workers which may be a bottleneck. Consider increasing the value of the `num_workers` argument` to `num_workers=3` in the `DataLoader` to improve performance.
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/lightning/pytorch/trainer/connectors/data_connector.py:424: The 'test_dataloader' does not have many workers which may be a bottleneck. Consider increasing the value of the `num_workers` argument` to `num_workers=3` in the `DataLoader` to improve performance.
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃      Classification       ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│     Acc      │          95.07%           │
│    Brier     │          0.07452          │
│   Entropy    │          0.19231          │
│     NLL      │          0.15997          │
└──────────────┴───────────────────────────┘
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃        Calibration        ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│     ECE      │          0.01316          │
│     aECE     │          0.01283          │
└──────────────┴───────────────────────────┘
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃ Selective Classification  ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│    AUGRC     │           0.39%           │
│     AURC     │           0.44%           │
│  Cov@5Risk   │          100.00%          │
│  Risk@80Cov  │           0.56%           │
└──────────────┴───────────────────────────┘

[{'test/cal/ECE': 0.01316485833376646, 'test/cal/aECE': 0.012833844870328903, 'test/cls/Acc': 0.9506999850273132, 'test/cls/Brier': 0.07451875507831573, 'test/cls/NLL': 0.15996992588043213, 'test/sc/AUGRC': 0.0039479900151491165, 'test/sc/AURC': 0.00444554490968585, 'test/sc/Cov@5Risk': 1.0, 'test/sc/Risk@80Cov': 0.005625000223517418, 'test/cls/Entropy': 0.19230850040912628, 'test/ens_Disagreement': 0.008258333429694176, 'test/ens_Entropy': 0.1914074420928955, 'test/ens_MI': 0.0009010148933157325}]

6. Testing the Model

Now that the model is trained, let’s test it on MNIST. Please note that we apply a reshape to the logits to determine the dimension corresponding to the ensemble and to the batch. As for TorchUncertainty 0.2.0, the ensemble dimension is merged with the batch dimension in this order (num_estimator x batch, classes).

import matplotlib.pyplot as plt
import numpy as np
import torch
import torchvision


def imshow(img):
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.axis("off")
    plt.tight_layout()
    plt.show()


dataiter = iter(datamodule.val_dataloader())
images, labels = next(dataiter)

# print images
imshow(torchvision.utils.make_grid(images[:4, ...]))
print("Ground truth: ", " ".join(f"{labels[j]}" for j in range(4)))

# Put the model in eval mode to use several samples
model = model.eval()
logits = model(images).reshape(16, 128, 10) # num_estimators, batch_size, num_classes

# We apply the softmax on the classes and average over the estimators
probs = torch.nn.functional.softmax(logits, dim=-1)
avg_probs = probs.mean(dim=0)
var_probs = probs.std(dim=0)

_, predicted = torch.max(avg_probs, 1)

print("Predicted digits: ", " ".join(f"{predicted[j]}" for j in range(4)))
print("Std. dev. of the scores over the posterior samples", " ".join(f"{var_probs[j][predicted[j]]:.3}" for j in range(4)))

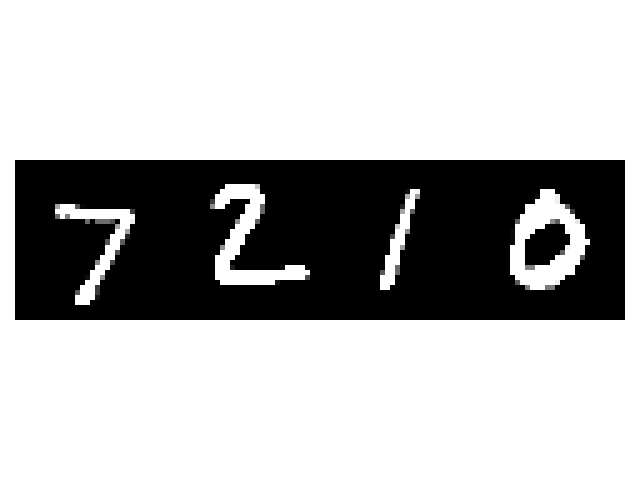
Ground truth:  7 2 1 0
Predicted digits:  7 2 1 0
Std. dev. of the scores over the posterior samples 0.00232 1.9e-05 0.000428 0.00775

Here, we show the variance of the top prediction. This is a non-standard but intuitive way to show the diversity of the predictions of the ensemble. Ideally, the variance should be high when the average top prediction is incorrect.

References

• LeNet & MNIST: LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE.

• Bayesian Neural Networks: Blundell, C., Cornebise, J., Kavukcuoglu, K., & Wierstra, D. (2015). Weight Uncertainty in Neural Networks. ICML 2015.

• The Adam optimizer: Kingma, D. P., & Ba, J. (2014). “Adam: A method for stochastic optimization.” ICLR 2015.

• The Blitz library (for the hyperparameters).