Training a LeNet with Monte Carlo Batch Normalization

In this tutorial, we will train a LeNet classifier on the MNIST dataset using Monte-Carlo Batch Normalization (MCBN), a post-hoc Bayesian approximation method.

Training a LeNet with MCBN using TorchUncertainty models and PyTorch Lightning

In this part, we train a LeNet with batch normalization layers, based on the model and routines already implemented in TU.

1. Loading the utilities

First, we have to load the following utilities from TorchUncertainty:

• the TUTrainer from our framework

• the datamodule handling dataloaders: MNISTDataModule from torch_uncertainty.datamodules

• the model: LeNet, which lies in torch_uncertainty.models

• the MC Batch Normalization wrapper: mc_batch_norm, which lies in torch_uncertainty.post_processing

• the classification training routine in the torch_uncertainty.routines

• an optimization recipe in the torch_uncertainty.optim_recipes module.

We also need import the neural network utils within torch.nn.

from pathlib import Path

from torch import nn

from torch_uncertainty import TUTrainer
from torch_uncertainty.datamodules import MNISTDataModule
from torch_uncertainty.models.lenet import lenet
from torch_uncertainty.optim_recipes import optim_cifar10_resnet18
from torch_uncertainty.post_processing.mc_batch_norm import MCBatchNorm
from torch_uncertainty.routines import ClassificationRoutine

2. Creating the necessary variables

In the following, we define the root of the datasets and the logs. We also create the datamodule that handles the MNIST dataset dataloaders and transforms.

trainer = TUTrainer(accelerator="cpu", max_epochs=2, enable_progress_bar=False)

# datamodule
root = Path("data")
datamodule = MNISTDataModule(root, batch_size=128)


model = lenet(
    in_channels=datamodule.num_channels,
    num_classes=datamodule.num_classes,
    norm=nn.BatchNorm2d,
)

3. The Loss and the Training Routine

This is a classification problem, and we use CrossEntropyLoss as likelihood. We define the training routine using the classification training routine from torch_uncertainty.training.classification. We provide the number of classes, and the optimization recipe.

routine = ClassificationRoutine(
    num_classes=datamodule.num_classes,
    model=model,
    loss=nn.CrossEntropyLoss(),
    optim_recipe=optim_cifar10_resnet18(model),
)

4. Gathering Everything and Training the Model

You can also save the results in a variable by saving the output of trainer.test.

trainer.fit(model=routine, datamodule=datamodule)
perf = trainer.test(model=routine, datamodule=datamodule)

/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/lightning/pytorch/trainer/connectors/data_connector.py:424: The 'val_dataloader' does not have many workers which may be a bottleneck. Consider increasing the value of the `num_workers` argument` to `num_workers=3` in the `DataLoader` to improve performance.
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/lightning/pytorch/trainer/connectors/data_connector.py:424: The 'train_dataloader' does not have many workers which may be a bottleneck. Consider increasing the value of the `num_workers` argument` to `num_workers=3` in the `DataLoader` to improve performance.
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/lightning/pytorch/trainer/connectors/data_connector.py:424: The 'test_dataloader' does not have many workers which may be a bottleneck. Consider increasing the value of the `num_workers` argument` to `num_workers=3` in the `DataLoader` to improve performance.
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃      Classification       ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│     Acc      │          97.80%           │
│    Brier     │          0.03355          │
│   Entropy    │          0.07697          │
│     NLL      │          0.06875          │
└──────────────┴───────────────────────────┘
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃        Calibration        ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│     ECE      │          0.00332          │
│     aECE     │          0.00237          │
└──────────────┴───────────────────────────┘
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃ Selective Classification  ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│    AUGRC     │           0.10%           │
│     AURC     │           0.12%           │
│  Cov@5Risk   │          100.00%          │
│  Risk@80Cov  │           0.08%           │
└──────────────┴───────────────────────────┘

5. Wrapping the Model in a MCBatchNorm

We can now wrap the model in a MCBatchNorm to add stochasticity to the predictions. We specify that the BatchNorm layers are to be converted to MCBatchNorm layers, and that we want to use 8 stochastic estimators. The amount of stochasticity is controlled by the mc_batch_size argument. The larger the mc_batch_size, the more stochastic the predictions will be. The authors suggest 32 as a good value for mc_batch_size but we use 4 here to highlight the effect of stochasticity on the predictions.

routine.model = MCBatchNorm(
    routine.model, num_estimators=8, convert=True, mc_batch_size=16
)
routine.model.fit(datamodule.train)
routine = routine.eval()  # To avoid prints

6. Testing the Model

Now that the model is trained, let’s test it on MNIST. Don’t forget to call .eval() to enable Monte Carlo batch normalization at evaluation (sometimes called inference). In this tutorial, we plot the most uncertain images, i.e. the images for which the variance of the predictions is the highest. Please note that we apply a reshape to the logits to determine the dimension corresponding to the ensemble and to the batch. As for TorchUncertainty 2.0, the ensemble dimension is merged with the batch dimension in this order (num_estimator x batch, classes).

import matplotlib.pyplot as plt
import numpy as np
import torch
import torchvision


def imshow(img):
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.axis("off")
    plt.tight_layout()
    plt.show()


dataiter = iter(datamodule.val_dataloader())
images, labels = next(dataiter)

routine.eval()
logits = routine(images).reshape(8, 128, 10)  # num_estimators, batch_size, num_classes

probs = torch.nn.functional.softmax(logits, dim=-1)
most_uncertain = sorted(probs.var(0).sum(-1).topk(4).indices)

# print images
imshow(torchvision.utils.make_grid(images[most_uncertain, ...]))
print("Ground truth: ", " ".join(f"{labels[j]}" for j in range(4)))

for j in most_uncertain:
    values, predicted = torch.max(probs[:, j], 1)
    print(
        f"Predicted digits for the image {j}: ",
        " ".join([str(image_id.item()) for image_id in predicted]),
    )

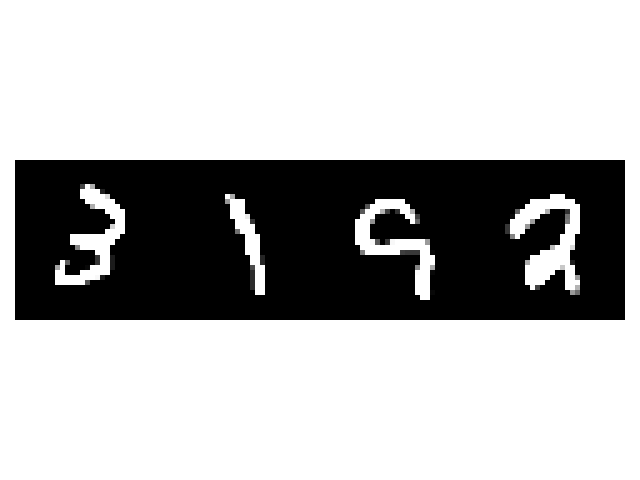
Ground truth:  7 2 1 0
Predicted digits for the image 63:  3 3 2 2 2 2 2 3
Predicted digits for the image 96:  7 1 1 1 1 7 1 1
Predicted digits for the image 104:  5 9 9 9 9 9 9 9
Predicted digits for the image 119:  2 2 2 2 2 2 2 7

The predictions are mostly erroneous, which is expected since we selected the most uncertain images. We also see that there stochasticity in the predictions, as the predictions for the same image differ depending on the stochastic estimator used.