Training a LeNet with Monte-Carlo Dropout

In this tutorial, we will train a LeNet classifier on the MNIST dataset using Monte-Carlo Dropout (MC Dropout), a computationally efficient Bayesian approximation method. To estimate the predictive mean and uncertainty (variance), we perform multiple forward passes through the network with dropout layers enabled in train mode.

For more information on Monte-Carlo Dropout, we refer the reader to the following resources:

• Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning ICML 2016

• What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? NeurIPS 2017

Training a LeNet with MC Dropout using TorchUncertainty models and PyTorch Lightning

In this part, we train a LeNet with dropout layers, based on the model and routines already implemented in TU.

1. Loading the utilities

First, we have to load the following utilities from TorchUncertainty:

• the TUTrainer from TorchUncertainty utils

• the datamodule handling dataloaders: MNISTDataModule from torch_uncertainty.datamodules

• the model: lenet from torch_uncertainty.models

• the MC Dropout wrapper: mc_dropout, from torch_uncertainty.models.wrappers

• the classification training & evaluation routine in the torch_uncertainty.routines

• an optimization recipe in the torch_uncertainty.optim_recipes module.

We also need import the neural network utils within torch.nn.

from pathlib import Path

from torch import nn

from torch_uncertainty import TUTrainer
from torch_uncertainty.datamodules import MNISTDataModule
from torch_uncertainty.models import mc_dropout
from torch_uncertainty.models.classification import lenet
from torch_uncertainty.optim_recipes import optim_cifar10_resnet18
from torch_uncertainty.routines import ClassificationRoutine

MAX_EPOCHS = 1
BATCH_SIZE = 512

2. Defining the Model and the Trainer

In the following, we first create the trainer and instantiate the datamodule that handles the MNIST dataset, dataloaders and transforms. We create the model using the blueprint from torch_uncertainty.models and we wrap it into an mc_dropout. To use the mc_dropout wrapper, make sure that you use dropout modules and not functionals. Moreover, they have to be instantiated in the __init__ method.

trainer = TUTrainer(accelerator="gpu", devices=1, max_epochs=MAX_EPOCHS, enable_progress_bar=False)

# datamodule
root = Path("data")
datamodule = MNISTDataModule(root=root, batch_size=BATCH_SIZE, num_workers=8)


model = lenet(
    in_channels=datamodule.num_channels,
    num_classes=datamodule.num_classes,
    dropout_rate=0.5,
)

mc_model = mc_dropout(model, num_estimators=16, last_layer=False)

3. The Loss and the Training Routine

This is a classification problem, and we use CrossEntropyLoss as the (negative-log-)likelihood. We define the training routine using the classification training routine from torch_uncertainty.routines. We provide the number of classes the optimization recipe and tell the routine that our model is an ensemble at evaluation time.

routine = ClassificationRoutine(
    num_classes=datamodule.num_classes,
    model=mc_model,
    loss=nn.CrossEntropyLoss(),
    optim_recipe=optim_cifar10_resnet18(mc_model),
    is_ensemble=True,
)

4. Gathering Everything and Training the Model

We can now train the model using the trainer. We pass the routine and the datamodule to the fit and test methods of the trainer. It will automatically evaluate some uncertainty metrics that you will find in the table below.

trainer.fit(model=routine, datamodule=datamodule)
results = trainer.test(model=routine, datamodule=datamodule)

┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃      Classification       ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│     Acc      │          79.360%          │
│    Brier     │          0.52871          │
│   Entropy    │          1.85231          │
│     NLL      │          1.16351          │
└──────────────┴───────────────────────────┘
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃        Calibration        ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│     ECE      │          43.005%          │
│     aECE     │          42.997%          │
└──────────────┴───────────────────────────┘
┏━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Test metric  ┃ Selective Classification  ┃
┡━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│    AUGRC     │          5.258%           │
│     AURC     │          7.081%           │
│  Cov@5Risk   │           nan%            │
│  Risk@80Cov  │          13.350%          │
└──────────────┴───────────────────────────┘

5. Testing the Model

Now that the model is trained, let’s test it on MNIST. Don’t forget to call .eval() to enable dropout at evaluation and get multiple (here 16) predictions.

import matplotlib.pyplot as plt
import numpy as np
import torch
import torchvision
from einops import rearrange


def imshow(img) -> None:
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.axis("off")
    plt.tight_layout()
    plt.show()


dataiter = iter(datamodule.val_dataloader())
images, labels = next(dataiter)
images = images[:6]

# print images
imshow(torchvision.utils.make_grid(images[:6, ...], padding=0))

routine.eval()
logits = rearrange(routine(images), "(m b) c -> b m c", b=6)
probs = logits.softmax(dim=-1)


for j in range(6):
    values, predicted = torch.max(probs[j, :], 1)
    print(
        f"MC-Dropout predictions for the image {j + 1}: ",
        " ".join([str(image_id.item()) for image_id in predicted]),
    )

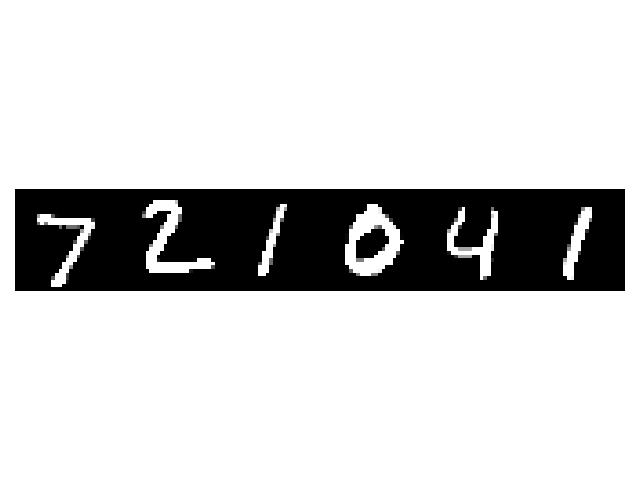
MC-Dropout predictions for the image 1:  7 7 7 7 7 2 7 7 2 7 7 2 7 2 7 7
MC-Dropout predictions for the image 2:  2 2 2 2 7 2 2 5 3 2 2 2 2 2 2 0
MC-Dropout predictions for the image 3:  1 1 1 1 1 1 7 1 1 1 1 8 1 1 1 1
MC-Dropout predictions for the image 4:  2 3 2 5 0 3 2 8 0 3 5 2 2 2 5 0
MC-Dropout predictions for the image 5:  4 4 1 4 4 3 4 4 4 4 4 4 4 4 4 4
MC-Dropout predictions for the image 6:  1 1 1 1 1 1 9 1 1 1 1 1 1 1 1 1

Most of the time, we see that there is some disagreement between the samples of the dropout approximation of the posterior distribution.